So teuer ist der Klebespaß: Die große Panini-Sticker Rechnung

Vom Schulhof bis in die Chefetagen: Ein 80-seitiges Heft, das darauf wartet, mit Bildern von Messi, Salah, Neuer, Lewandowski, Suarez und Co. gefüllt zu werden, ist momentan Objekt der Begierde in den verschiedensten Freundeskreisen und Altersklassen. Dem ersten, der erfolgreich sein Panini-Album gefüllt hat, sind Ruhm und Verehrung seiner Freunde oder Kollegen gewiss - und zwar egal, ob der Sammler 8 ist oder 48.
Mit Hilfe der Wahrscheinlichkeitsrechnung
Mathematisch betrachtet verhält es sich so: Ein volles Heft hat 682 Sticker. Verkauft werden Packungen zu fünf Stickern um 90 Cent pro Packung. Unsern Beispiel-Sammler nennen wir Klaus. Möchte Klaus ohne Tauschen das Heft voll bekommen, muss er laut Wahrscheinlichkeitsrechnung 4.832 Pickerl kaufen, das entspricht 967 Packungen um saftige 870,30 Euro.
Da der Gedanke an diese Summe vielen Eltern sammelwütiger Kinder das Fürchten lehren dürfte, nehmen wir nun einmal an, Klaus tauscht mit neun weiteren Freunden. „Durch eine ziemlich komplexe Rechnung erschließt sich, dass jeder der zehn Sammler dann 314 Packungen kaufen müsste, also 282,27 Euro zahlen“, erklärt der Mathematiker Helmut Hofbauer.
Das klingt schon besser. Und wenn Klaus einfach 682 Sticker kauft? Hofbauer rechnet vor: Die Wahrscheinlichkeit, dass der erste Sticker passt liegt bei 100 Prozent (682 durch 682). Die Wahrscheinlichkeit, dass die ersten beiden Sticker passen ist 682/682 * 681/682=99,85 Prozent. Wenn man nun möchte, dass 682 Sticker gleich passen, dann ergibt sich folgender Ausdruck:
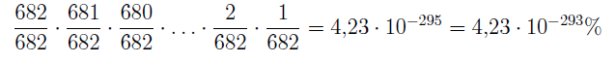
Das bedeutet, die Wahrscheinlichkeit, mit 682 gekauften Stickern ein Heft füllen zu können, ist so gering, bzw. hat das Ergebnis so viele Nullen, dass der Taschenrechner der Einfachheit halber gleich 0 Prozent anzeigt.
"Ich hab so viele Doppelte"
Panini gibt an, alle Sticker gleich oft zu drucken. Aber wie viele Sticker kann Klaus kaufen, bis die Wahrscheinlichkeit, einen doppelten Sticker zu erhalten, über 50 Prozent liegt?
Um diese Anzahl x zu errechnen, benötigt man laut Hofbauer nachfolgende Gleichung, wobei i eine Laufvariable ist und die natürlichen Zahlen vom Startwert 1 bis zum Endwert x in den nachfolgenden Term einsetzt. Das große Pi gibt an, dass diese einzelnen Terme miteinander multipliziert werden, was auf dem selben Prinzip beruht wie die obige Wahrscheinlichkeitsberechnung.
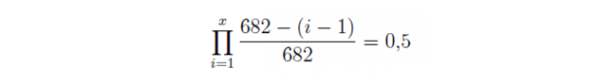
"Demnach erhält man mit 50%iger Sicherheit bei den ersten 31 Stickern bzw. 6 Packungen keine Duplikate. Nur mehr ein Prozent beträgt die Wahrscheinlichkeit, dass unter den ersten 78 Stickern keine Duplikate vorkommen“, erklärt Hofbauer die Rechnung.
Für den Sammler, der meint, er habe es bald geschafft und das Heft wäre gleich voll, gibt es schlechte Nachrichten aus der Welt der Mathematik: Für die letzten 19 Sticker benötigt man laut Wahrscheinlichkeit die gleiche Anzahl an Packerln wie für die ersten 663 Sticker. Zur Not gibt es für diesen Fall eine unter Sammelfreunden zwar verpönte, aber wirkungsvolle Methode: Um 25 Cent pro Sticker (plus Versandgebühren) kann man die Bilder einzeln bei Panini bestellen.
Im Album kleben übrigens 95 falsche Spieler, da Panini schon lange vor der Kaderbekanntgabe druckt.
Kommentare